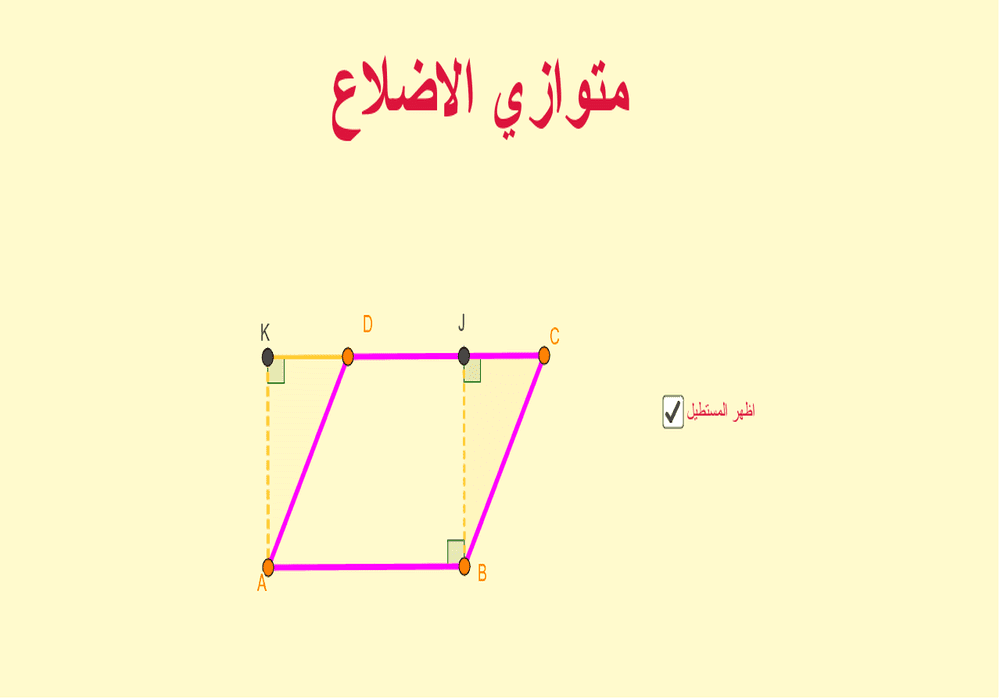
قانون مساحة متوازي الاضلاع

قانون مساحة متوازي الاضلاع متوازي الأضلاع أحد الأشكال الهندسة المميزة الذي دراستها في مجال الهندسة والمعمار يتميز متوازي الأضلاع أن لديه 4 أضلاع كل ضلعين متساويين ومتوازيين سوف نتعرف عبر موقع زيادة من خلال مقالنا عن.

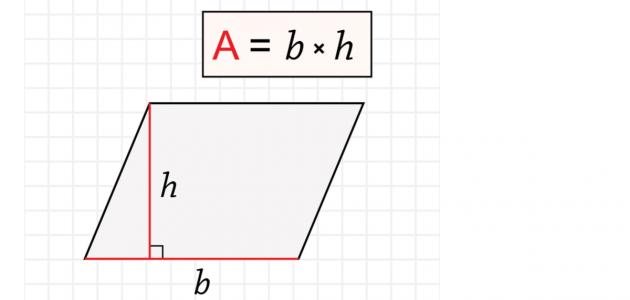
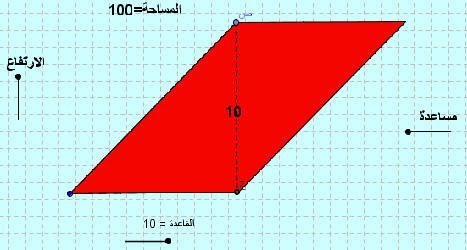
قانون مساحة متوازي الاضلاع. قانون مساحة المثلث متساوي الأضلاع. نظرة عامة حول المثلث متساوي الأضلاع. مساحة متوازي الأضلاع طول القاعدة الارتفاع. بتطبيق قانون مساحة متوازي الأضلاع طول القاعدة الارتفاع ينتج أن.

مساحة متوازي الأضلاع 11 8 88سم. قانون مساحة متوازي الاضلاع. أوجد مساحة متوازي الأضلاع إذا علمت أن طول أحد أضلاعه 5 سم وطول العامود. أمثلة على حساب مساحة المثلث متساوي الأضلاع.

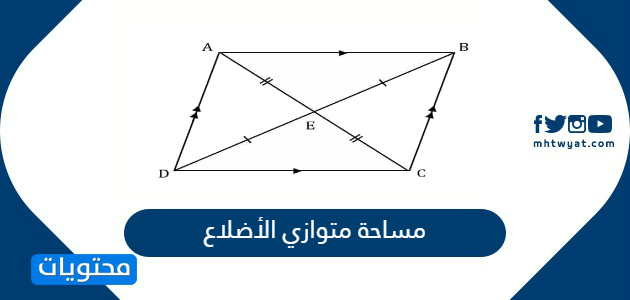
قانون مساحة متوازي الأضلاع عبر موقع محتوى متوازي الأضلاع بالإنجليزية يعني parallelogram وهو شكل هندسي له أربعة أضلاع يمكن اعتباره مستطيل أو مربع أو معين إذا حقق بعض الشروط التي سوف نذكرها لاحقا فتعالوا نتعرف عبر موقع. كل قطر في متوازي الأضلاع منصف للقطر الآخر. مساحة متوازي الأضلاع تساوي ضعف مساحة المثلث المشكل بضلعين وقطر. إن مساحة متوازي الأضلاع م تساوي طول القاعدة ل مضروبا بالمسافة العامودي ة بين القاعدتين ع ويمكن تمثيلها بالر موز الر ياضي ة على الشكل م ع ل كما أن هناك.

إذا كانت طول قاعدة متوازي الاضلاع يعادل 3 أضعاف ارتفاعه ومساحته 192سم فما هو طول قاعدته وارتفاعه. مساحة متوازي الأضلاع. المراجع نظرة عامة حول المثلث. التعرف على قانون حساب مساحة متوازي الأضلاع.

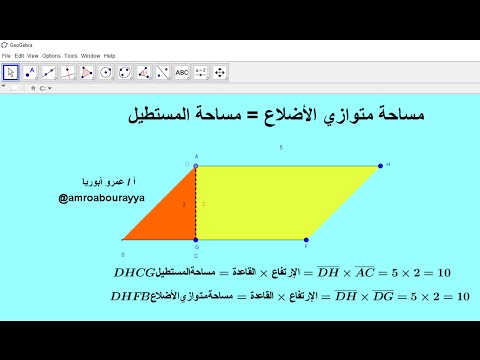
متوازي الاضلاع شكل ثنائي الابعاد و كل شكل ثنائي الابعاد يمكن حساب مساحته و محيطه و لاستنتاج قانون لحساب مساحة المعين قام العلماء بتجزئة متوازي الاضلاع الى مثلث و مستطيل و قد توصلوا الى ايجاد صيغة لقانون يمكن عن طريقه. قانون مساحة متوازي الأضلاع مساحة متوازي الأضلاع بدلالة القاعدة. يتقاطع قطراه في نقطة تشكل مركز تناظر لمتوازي الأضلاع وتسمى مركز متوازي الأضلاع. إذا كان ارتفاع متوازي الأضلاع غير معروف فيمكن استخدام علم المثلثات للعثور على المساحة حيث تصبح المساحة ab sin x حيث a و b هما طولا ضلعين متلاقيين في المتوازي و x هي الزاوية.